Stagnation as an excuse for sustained high P/E

Bubbles will arrive before inflation

When I was six or so, I had an idea that many other kids – and many of you – probably have also arrived to. If one may buy anything for the money and someone is able to print the money, why doesn't he print an unlimited amount of money in order to make everyone happy and solve all the world's problems?

The Keynesians and similar folks believe that this is a great idea even when they are adults. But many of us have managed to figure out – or were told – why this isn't such a great idea. After all, the nominal information expressed in the units of currency means nothing. A dollar or a crown or a deutschmark is just a lame unit of wealth. If everyone owns 10 times greater an amount of money, everyone will also demand a higher price for his goods and services.

So I quickly realized that the fact that a dollar was 30 times greater than the Czechoslovak crown was just an inconsequential choice of the units, just like the difference between meters and feet. One may design physically and socially equivalent situations by simply multiplying all the prices by \(C = \exp(\lambda)\) – by reducing the money by the factor of \(C\).

This "financial gauge invariance" may be used even for a single currency which evolves in time. You may rescale all the prices and related quantities expressed in the units of currency, \(P_i\), by a function of time \(t\),\[

P_i\to P'_i= C(t)\cdot P_i = \exp[\lambda(t)] P_i

\] and it's quite possible that nothing really changes. There are things like "rates" – interest rates, inflation rates, and so on. They're defined as the time derivatives of some quantity \(P_i\) divided by the quantity itself. So if you switch from the numerical value \(P_i\) to \(P'_i\), the new rate will be\[

\eq{
\frac{1}{P'_i}\cdot\ddfrac{P'_i}{t} &= \ddfrac{\ln(P'_i)}{t} =\\
&=\frac{1}{P'_i}\ddfrac{\zav{\exp[\lambda(t)] P_i}}{t} = \\
&= \frac{1}{P_i} \zav{\ddfrac{P_i}{t} + P_i \ddfrac{\lambda(t)}{t} }
}

\] by the Leibniz rule (for the derivative of a product).




The first term on the right hand side is nothing else than \(\dd \ln( P_i)/\dd t\), the old "rate", but there is one more term, \(\dd \lambda(t)/\dd t\): old rates are additively shifted by this universal quantity.

This shift is mathematically analogous to the transformation of charged fields and the gauge fields under the \(U(1)\) gauge symmetry in physics. All the charged fields get multiplied by \(\exp[i\lambda(x,y,z,t)Q]\) while the gauge field, analogous to rates, is shifted by \(e\partial_\mu \lambda(t)\).

The only different feature of the "financial gauge invariance" is that the argument of the exponential contains no imaginary unit \(i\). This difference means that the gauge group isn't really \(U(1)\) but its noncompact version, \(\RR^+\), the multiplicative group rescaling all the prices at time \(t\) by a positive factor. In fact, Hermann Weyl has introduced this \(\RR^+\) gauge symmetry (rescaling the distances, not prices) to the physics of general relativity, too. String theorists doing perturbative calculations use the Weyl symmetry (on the world sheet, in their case) all the time.




I am not saying that the "financial gauge invariance" implies that any procedure whose goal is to change the inflation rate will create a physically equivalent situation and that it will be inconsequential. I am saying that it's possible to have physically equivalent situations with (arbitrarily, vastly) different inflation rates. All the prices will get rescaled; all the rates (including all the interest rates) will get an extra additive universal contribution of the "enhanced inflation".

It's my feeling that many people, especially the Ron Paul types, don't quite get this gauge invariance – the point that the numerical value of the prices and even its change in time doesn't really matter.

That's a good initial insight but for some years, I as a kid didn't make much progress in understanding the world of the finance. For quite some time, I was assuming that there was only one interesting "rate". It was the inflation rate mixed up with the interest rate, and so on. The discount rate was probably the same thing, I would be thinking if I were told something about the discount rate. There may also be some "real GDP growth rate" but I wasn't thinking about its impact on the logic of the finance much. It took a long time for me to appreciate that these rates are different in general and the differences are extremely important. In particular, banks are increasing the interest rates if they want to lower the inflation rate and (much more likely these days) vice versa.

A closely related basic example: the interest rate on your saving account isn't the same thing as the inflation rate. In some "ideal world", you could be promised that they are equal – a vanishing real interest rates. But the real world is not an ideal one; these two rates may differ. A central bank may be legally obliged to target the inflation rate (the interest rates may only be specified after the inflation is calculated – unless we use a predicted inflation – so there may be a delay). But the central bank may also creatively change the interest rate so that the "real interest rate" is nonzero. The real interest rate (nominal interest rate minus inflation rate) has been negative in most Western countries for many years.

At the beginning, I wanted to convince you that the "nominal rates" don't really mean anything – physically equivalent situations related by the "financial gauge invariance" may have rates differing by an arbitrary function of time. But now we see that the difference between two rates is physical. The real interest rate is an example. If it is positive, the savers are getting "really richer"; if it is negative, it's the other way around.

This opens many basic yet important questions: Can the central banks really influence the real interest rates? If they can, isn't it always a counterproductive market intervention that makes the economy less efficient? In principle, can the free market determine the real interest rates by itself (in an idealized world that is naturally identified as a "world without government interventions")? What are the drivers that determine its value?

The answer to the first question is Yes, a central bank may influence the real interest rates. The central banks define the interest rates paid on the commercial banks' reserves. For banks, it may be a better idea to lend the money to real-world people and companies, at a higher interest rate, so you could think that the interest rate on the reserves is irrelevant. However, a fraction of the bank's holdings must be in cash – the actual reserves, banknotes – so the interest rate paid on these reserves does influence what the bank may pay to the savers.

In most countries, laws define "reserve requirements" that guarantee that a bank doesn't go bust well before someone notices that something is wrong. Between 3 and 30 percent of the banks' holdings are required to be in the form of actual banknotes or the reserves. So the rate on the reserves determined by a central bank does determine what you get on your saving account, too, although the expected influence is smaller than the change of the central interest rate (essentially by the fraction that says what part of the banks' holdings are kept as safe reserves).

The second question was whether the central banks should try to "engineer" the "right" real interest rates. Keynesians surely answer "Yes". They view the central banks as a miraculous part of the government that can make everyone happy. I, as a free-market advocate, realize that the engineering of real interest rates is de facto a form of wealth redistribution. If you lower real interest rates by an intervention, you de facto make the savers poorer and you defend this step by helping someone else. That's the reason why I agree with the Tea Party types that a central bank shouldn't be active in this way.

But it's important that I am talking about real interest rates, not the nominal ones. Nominal ones don't really matter for the real world. They are not gauge-invariant.

For these reasons, I find the inflation targeting to be among the most neutral monetary policies. Along with some similar policies, it involves the least amount of redistribution of the "real wealth". This anti-socialist virtue is almost equivalent to another virtue: it makes the currency unit as predictable as possible and in average, it's good for everyone. The amplitude of oscillations is minimized. The amount of "lottery" in your financial results is reduced. In other words, the correlation between "good work" and "income" is maximized. Whatever the detailed policy is, I think it is healthy if the central banks have as little influence as possible, if the policies are "automatized". As a bonus, this condition automatically reduces the room for inside trading and speculations (those that are unproductive for the society), too.

Drivers affecting the real interest rates

Can the market determine the real interest rates by itself? What do they mean if we imagine that the government interventions are eliminated (in particular, you can't borrow from the government and you don't lend to the government, or at least the government is treated just like "another company" trying to maximize its well-being rather than an omnipresent institution intervening into the markets)? Well, borrowers offer low real interest rates if it is easy for them to borrow the money elsewhere – if the lenders have a lot of competition. And vice versa: Lenders may achieve high returns if many people want to borrow, and if they badly want to borrow. In other words, the real interest rates are high if there is a competition between borrowers, if too many people want to borrow. And vice versa: they are low if no one wants to be in debt.

(Their being near zero today is a sign that people and companies are (relatively) afraid of creating new debt. Savers have a special, sensible reason for that: they feel that they are poor and will be poorer. They can't afford to spend too much. At least when it comes to savers, policies trying to hurt them and discourage saving actually reduce consumption. The chronic borrowers are encouraged to borrow by low interest rates but it comes with a price – an increased risk of insolvency.)

The paragraph starting with "Can" explains how a healthy economy should decide about the real interest rates. Real interest rates should be determined by the balance between the supply and demand, too. If people want to save (and lend) too much, the market automatically discourages them because with too many fellow savers (and lenders), the real interest rates go down due to the competition and the saving (and lending) becomes less attractive. And on the contrary, if too many people get mad and start to borrow too much, there is a competition between them which allows the lenders to increase the real interest rates. This ultimately discourages the borrowers from borrowing.

Because of this simple mechanism – one that is fully analogous to the invisible hand's ability to dictate the right prices of everything and anything – the market knows best whether it's right for the savers to lose the money in the real terms or not. It seems to me that the world's economy is so brutally distorted by the Keynesians that most people don't even realize what I wrote in the previous paragraphs of this section – i.e. how the markets should decide about the real interest rates in an ideal world (and that they have a solid, "automatic" mechanism to do so at all). In fact, I think that even central bankers who are typically drowning in the ocean of the Keynesian feces fail to understand the right mechanisms that should decide about the real interest rates – and that normally protect the economy from oversaving as well as overborrowing. We clearly live in an overregulated world in which Keynesian and other ad hoc superstitions largely overshadowed something that I would consider the textbook knowledge about economics – e.g. that the market determines relative prices and rates most efficiently and most safely.

Particular distortion by the central banks in the recent years

The central banks kept on inventing all sort of Keynesian and quasi-Keynesian excuses for various random distortions of the market. Because the free market is the best tool to decide about the optimal allocation of the capital and all prices and (real) interest rates, any intervention that distorts the prices and interest rates reduces the efficiency of the economy.

This comment would apply regardless of the "sign". However, we live in a particular era and in recent years, the economies were distorted in a particular direction. I think that everyone knows what the direction was. The central banks were printing tons of money, pumping them into the economy. They were pushing banknotes to the people's throats (assuming that this will make the people more hungry), intervening, and trying to "punish the savers" by steps artificially lowering the real interest rates as much as possible. The interventions took the form of keeping the interest rates near zero or at zero and other non-standard procedures. Some of the non-standard procedures (like QE) don't really matter. Others, like the interventions against the Czech crown, surely matter but only locally – distorting the Czech economy exactly in the opposite way than what is their (more diluted) impact on the eurozone (euro reserves were being piled by the Czech Central Bank for a few weeks: about EUR 8 billion were bought for freshly printed Czech banknotes).

The motivation for this artificial loosening is a (partly irrational) fear of a recession and the obsession with the positiveness of the GDP growth rate, regardless of the fact that much of the added GDP results from an increased debt (a thing that one should really be worried about much more than about a smaller GDP growth) and from various tricks that imply that much of the activity in the GDP is really "fake".

At any rate, these interventions have had no severe consequences yet – like hyperinflation. Everything looked like a relatively smooth sailing. But something has been changing about the underlying numbers. Look at these scary graphs from Harvard's PolicyMic:



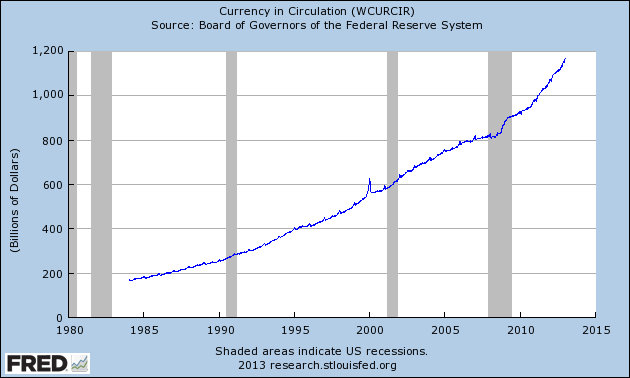
Between early 1980s and now, the currency in circulation increased 7-fold or so, to $1.2 trillion. Clearly, this growth by the factor of 7 vastly exceeds the increase of the GDP, even the nominal one. At least, the graph above looks uniform and sustainable. But there are more shocking graphs.



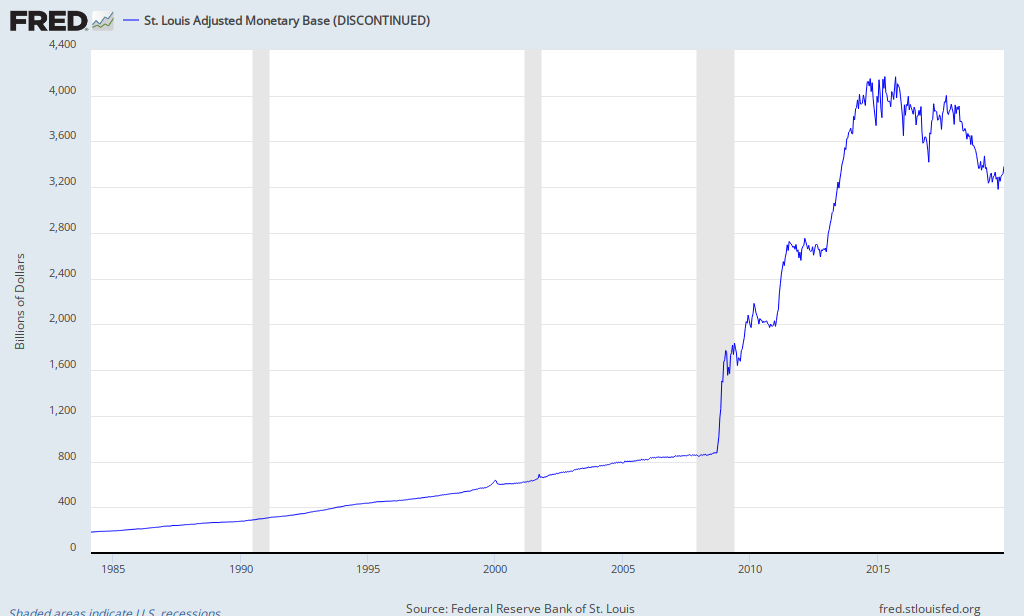
This is the St Louis adjusted monetary base that contains not only the banknotes and coins in circulation but also the commercial banks' cash reserves, roughly speaking. Since 2009, just in four years, it grew by a factor of 4 or so. That more or less means that the commercial banks' cash reserves have grown dramatically.

This huge, four-fold relative increase of the monetary base in 4 years certainly hasn't led to a quadrupling of prices. The prices in the U.S. have barely changed and the GDP growth has been minor, too. If you just print lots of banknotes and lock them in the basement, they will not influence anything. And that's really what was more or less happening so far. The dramatic increase of the monetary base above didn't mean much because it's mostly spurious. Banks' balance sheets were increasing, much of their assets are kept as reserves, these reserves are included into the monetary base graphed above, but the increased debt of the banks isn't counted even though it really "cancels" the increased reserves.

The monetary policies have largely affected the flows of loans between the arms of the government and banks only – the real-world loans of the real-world people are determined by other things than the government apparatchiks' proclamations.

Those procedures behind the quantitative easing are the ultimate prototype of the interventions that shows why these interventions are slightly counterproductive but more clearly, futile. The goal of all these interventions, the printing and pumping of the money, is to accelerate the real economy. However, much of the extra money that is being printed and pumped remains locked in basements and they influence nothing. They only influence mostly unphysical (thank God, so far) graphs like the St Louis monetary base graph above.

The real economy isn't affected much (or detectably) for a simple reason: The desire of the actual people to lend and borrow isn't actually affected by extra banknotes that appear in the basements. It's determined by the free market, by the balance of the supply and demand – i.e. ultimately by the people's desire (or need) to save and lend or, on the contrary, borrow. As I have argued at the beginning, most of the real interest rate is dictated by the people's own situation and psychology, by the balance of the supply and demand (real-world lenders and real-world borrowers and how they evaluate the importance of the debt and the risks). The "activist", Keynesian manipulation with the interest rates only influences a small part of the interest paid on savings (the percentage equal to the percentage of banks' assets that are or have to be kept as reserves). The rest – the majority – is unaffected by the central banks' interventions.

Similarly, operations such as QE only distort some relative prices, relative interest rates i.e. the detailed shape of the yield curve and they redistribute the wealth in some way, creating some losers and some winners (according to what they were holding and what they are going to buy). But they don't really change anything about the "total activity" in the economy and any redistribution reduces the efficiency and fairness of the economy which ultimately reduces the GDP (by terms of second order in the magnitude of the intervention).

So thankfully, much of the misguided activity of the central banks has only affected "mostly spurious" graphs such as the monetary base in the graph above. So far. But the purpose of all this loosening and interventions has always been that the money will eventually be flushed out of the basements and they will get to real economy. Will they? There are trillions of dollars waiting in various basements that haven't really begun to circulate in the real economy but they were printed with the purpose to circulate ($4 trillion in the semi-locked basements is like 3 average monthly salaries waiting to be donated to each American including infants). Lots of things could change – and a huge inflation could start – if the original goals started to materialize.

I think, surprisingly, that the answer to the question "Will they?" above will depend on the collective thinking of the people which isn't quite predictable. If the people were thinking in a particular way, they just wouldn't care about the extra trillions in banknotes that are waiting in the basements. In effect, the Federal Reserve and other central banks may keep on printing obscene amounts of money but they will remain locked in the basements because people's "hunger" isn't really affected by the amount of food that they may buy and that is waiting in a basement. Balance sheets may be increased by balance sheets mean nothing – it's some equity that is immediately subtracted from itself to yield zero.

However, at some moment, inflation expectations are probably bound to emerge. A sufficient, critical amount of people will start to realize that due to the interventions, it's just a question of "when", not "whether", for the money to get out of the basements. Once a person who is effectively deciding about some reserves – even cash that he has borrowed – realizes that the banknotes will lose their value sometimes in the (foreseeable) future, he will start to get rid of them and convert them to something.

Once this motion starts, people will notice and an increasing number of people will bet that this trend is inevitable and it's time to get rid of the money. So I would say that we may have been in an equilibrium in which the continuing printing didn't matter but it's an unstable equilibrium because the banknotes are not hermetically locked in the basements and there is a risk that due to a perturbation, trillions of dollars will be flushed out in an unstoppable avalanche. (A future avalanche is the only possible ultimate result of some policies that hugely change some underlying graphs like those above but have virtually no effects on the real economy for a few years. That's why dangerous imbalances and instabilities are the only possible result of similar interventions – an explanation why the government should always better f*ck off, to put it very mildly.)

Because of this risk, some people are bound to think that this risk is a reality which means that they will effectively start the avalanche themselves. The apparent equilibrium we have been seeing for years – the Keynesian distortions of the financial markets by the activist central bankers – is an unstable one. It will start to collapse at some point and the instability will be only stoppable by a dramatic increase of the interest rates that the central bankers – who have been insanely dovish – won't have enough courage to set. Because of the limited influence of the central interest rates on the real-world interest rates, they could very well need 20% central interest rates to help to achieve 10% real-world interest rates that may be needed. Such a spike would produce an inverted yield curve that would lead to negative yields for some timescales in the future. All these things are problematic.

So if you agree that the money is not quite "hermetically" isolated and there's a risk that it will be flushed out due to a perturbation, you should agree that the process by which they will be flushed out is inevitable at some point and the only remaining question is where they will flow from the basements at the beginning.

I think that inflation – quickly increasing prices of common products and services – is likely if not guaranteed to arise. But I think that this won't be the first manifestation of the "semi-locked" money in the basements. Why? Because people's desire to spend the money for common goods and services is not directly affected or determined by the central banks' distortion of the financial markets.

Instead, they have a pretty much intrinsically, psychologically dictated level of desire to save and ensure themselves for the future, or to borrow. Because the "real spending" won't be affected, the risk of a deteriorating value of the money will mean that they will convert their cash to some other investment which is not "obviously" threatened by the flood that will flush out the cash from the basements.

So I tend to think that various bubbles in equities – stocks and perhaps real estate – will emerge before the inflation. People will first realize that it's safer to convert the cash holdings into a different form of investments. The flood from the basement will go into these other investments which will increase their value but not to "real spending", i.e. to everyday products and services which will continue to be unaffected.

In other words, bubbles will grow before the inflation will kick in. You might argue – especially if you look at Dow Jones above 16,000 etc. – that the bubbles have already begun to grow.

However, the word "bubble" implicitly means that we expect it to pop. My bonus point is that it doesn't have to be necessarily the case. Because of this flood of printed money, we may enter a long era in which the price-to-earnings ratio, P/E, will be much greater than the values we have been used to. If that long-term change materializes, people will effectively be gradually switching to stocks (and equivalent investments) as the money. An increasing number of people will hold their wealth (even borrowed cash) in the form of stocks which may continue to grow for quite some time.

Only once many of these people will find out that they're really richer, they may start to "really spend" and inflation will kick in.

So I am suggesting that P/E may be higher than the usual values of order 10 for many years. We must ask the question: What market forces dictate P/E?

Well, if a company is expected to grow and/or the recent earnings are seen as downward flukes, P/E may be much higher than 10. On the contrary, if a company is apparently declining or at risk to go bust, P/E may be much smaller than 10. Companies that are "guaranteed" to exist for many more years tend to have a higher P/E and vice versa. And of course, an unjustified bubble may inflate P/E, too. You might also think about antibubbles if you wish.

The basic logic that determines that some companies have a higher P/E than others is pretty clear. But what about the overall or average P/E? I used the number 10 in the previous paragraph which was mostly random but why is it 10? Can't it be a completely different number like 2 or 50? What is a company really worth?

Well, a company is a tool to produce profit. It has an expected lifetime. If you own stocks, you will get all the dividends from this expected lifetime. So P/E is "comparable" to the number of years over which the company will produce the dividends "comparable" to the last ones. If the company's profit will be halved every year, it will only generate a finite amount of profit in the whole future (equal to 2 years of the initial profit rate). A company that will last for "centuries" may be programmed to produce an infinite (total) amount of money in the future. But it's not a good idea to be too certain about the very far future, like 30 years from now, and a particular person whose lifetime is finite will be getting the income for a limited amount of time, anyway.

These are some of the hand-waving arguments why it is strange for P/E to exceed values like 30 or at least 50. But are these arguments waterproof? Can't the numbers be changed to totally different values because of the flood of trillions of dollars that will be flushed out of the basements?

I think that they can change, even in a (semi-)sustainable way.

The average or typical P/E may very well grow arbitrarily high, at least in principle. (In that case, the P/E ratios should increase globally – otherwise there would be clever transactions that would tend to make the P/E more uniform, anyway.) What would it mean and why would it be sustainable?

Well, if the people will start to decide that the cash is doomed, they will have an increasing fraction of their wealth, even "cash", in the form of stocks. To understand the idea, we may imagine that people will keep 90% of their salaries and all the savings in stocks and everyone will try to buy a "fair basket" or an "index fund" of stocks for most of his money. If that's so, the short-term fluctuations of the stock prices will be reduced. People will be effectively using the stocks or (approximately speaking) index funds as currency.

Once this trend reaches the people buying the everyday products and services are used to calculate the inflation rate, the inflation (growth of prices in the original currencies) will kick in. But there won't be any significant inflation if the prices are expressed in the "new currency" or "new currencies", the index funds.

If the average P/E reaches 100, it will still mean – in some careful interpretation – that the accumulated expected income from the company is equal to 100 years of recent dividends. But the reason why it's 100 won't be that something has fundamentally changed about the resilience of the companies etc. Instead, it will mean that the income is generated in the inflating old currencies such as dollars and this income is expected to grow.

If you knew that the inflation will be high (100%) but the interest rates will be kept at zero, and company's "real profit" is constant, to assume a simple situation, the company will produce something like 31 times recent dividends in the next 5 years (exponential growth etc.) So this is a justification for the P/E of the company to be vastly higher than just the number of years for which it is going to produce the same profit. Note that the condition needed for this increase of the "natural P/E" is the expectation of very low real interest rates for several years. Such conditions may justify higher stock prices (higher P/E). These sentences and this paragraph are therefore the most relevant ones for the claim promised in the title of this blog post. (In the real world, the real interest rates will not be of order –50 percent like here but closer to zero – but we may extrapolate companies to more than 5 years and the inflation [more precisely, loss of real wealth in savings] over the expected lifetime of the company may still be substantial.)

It's also sensible to expect a higher P/E in the environment of very low interest rates on savings because the dividends are successfully competing with the low interests even if these dividends are low.

So I do expect some rather dramatic changes in the years to come – changes that will result from the insanely loosened policies of the recent decade and something, especially the last 5 years. But I also do think that this will lead the people to de facto switch to different units of wealth that don't inflate that much so it won't be the end of the world. In fact, it's possible that nothing will change legally and the U.S. dollars etc. will continue to exist. Just the people's habits about how they store their holdings at various timescales may be vastly different than today and this will also mean that the numerical values of prices and even P/E may be very different than today.

Note that people rationally abandon units of currency whose value is decreasing too quickly (due to inflation) because it's dangerous to hold such "money". But when the value of some "coins" increases too much (deflation), it stops circulating as well because it's stupid to get rid of such a permanently growing miracle object (and it's better to keep it in the mattress than to lend it for zero or negative interest rates). In effect, only units of wealth whose inflation rate is "sufficiently" close to zero (which may perhaps include 10%) are picked by rational market players as something that is good to be used for payments for extended periods of time.

To summarize practical implications of the ideas above: I don't think that 16,000 is the end of the growth for Dow Jones, among related forecasts. The inflation will ultimately arrive to much of the world but equities should grow earlier and in the extended process of this growth, we may see a quasi-sustainably elevated P/E. This new, unusual regime isn't "quite" sustainable because at the end, the inflation will be tamed and there will be some ordinary real growth again.

The invisible hand spanks the government and restores some justice

You might interpret my point as a claim about the "long-term justice" that the invisible hand of the free markets is able to impose despite the distortions by the government. The observations can't guarantee that an investor will find the right timing for all transactions; he may be lucky or unlucky. But if the government or the central bank manages to artificially reduce the real interest rates – and especially their expectation – (well) below zero, it automatically means that the justifiable P/E ratio becomes (much) higher and stocks should be growing exactly when the expectation about the real interest rates in the future (comparable to the companies' lifetime) deteriorates. Once the expectation about the real interest rates improves again, the justifiable P/E decreases again and the bubble may pop. But it was not really an irrational bubble; there was a rational reason why the P/E was higher. As a result, the investor with an appropriately "averaged" portfolio cannot be punished by the government's interventions designed to punish investors, at least not in the long run. The government may only achieve a redistribution, a (more or less random) transfer of wealth from some people to others.