Electron electric dipole moment: moderately natural SUSY may come in 2015

Three weeks ago, the ACME collaboration (Jacob Baron et al.) improved (i.e. reduced) the previous, 2012 best limit on the electron's electric dipole moment by a factor of \(12\) (and by 3 orders of magnitude relatively to TRF 2011) in the article

Order of Magnitude Smaller Limit on the Electric Dipole Moment of the Electron

The experiment looks like this (click to zoom in):



OK, some exotic thorium monoxide molecules (which have the strongest known "internal" electric fields) with optical pumping via lasers in electric and magnetic fields are changing and the (produced) photons are (or could be, if they were produced) measured. Readers interested in the clever experimental setup will have to find a better source. Physics World, The Register, HuffPo, SciAm, and other semipopular media that covered it didn't discuss the method too much, either.

First, let us ask: What is the dipole moment that is being measured and how large is it?




Generally, at the high school level, an electric dipole is a pair consisting of a negative charge \(-Q\) at \(\vec r = 0\) and a positive charge \(+Q\) at \(\vec r=\vec r\), if you forgive me a tautology (the meaning of the two \(\vec r\) symbols is different). In that case, the magnitude of the electric dipole is\[

\vec p = Q\cdot \vec r.

\] Its magnitude is \(Q|\vec r|\); its direction agrees with the separation of the two charges (from minus to plus). For more general charge distributions, the dipole is\[

\vec p = \int \rho(\vec r) \vec r \,\dd^3 r.

\] You may notice that this depends on the choice of the origin of coordinates (it changes when we shift the coordinates by a constant) unless the total charge \(\int \rho \,d^3 r=0\). If the total charge is nonzero, the electric dipole moment defined above may be changed to "anything" (any vector) after an appropriate shift of the coordinates.




That's bizarre because the total electric charge of the electron is nonzero. So what can we possibly mean by "the" electric dipole moment of the electron? The answer is that we use the definition above and require that the origin of the coordinates agrees with the center of mass of the electron. In effect, the "center of the charge distribution" is shifted relatively to the "center of mass" of the electron. And this distance (vector) multiplied by the electron charge is the electric dipole moment of the electron.

It is linked to the spin and small

But the dipole moment is a vector; what is the direction of the vector? Is it some preferred direction in the Universe? Does the vector point to Mecca? Well, no. Mecca doesn't define any preferred direction and a billion of people who believe otherwise can't change this fact. There is no preferred direction in the Universe.

The direction of the dipole moment \(\vec p\) has to be correlated with a preexisting direction in our situation. The situation only contains the electron and the only vector-like, directionful information that the electron has is its spin. So \[

\vec p_e = C\cdot \vec S.

\] In particle physics, we like to derive all the equations of motion and dynamics from the Hamiltonian (a fancy name for the total energy) or the Lagrangian. What is the energy of an electric dipole? Well, you just sum the electrostatic potential energy \(Q\phi\) from the charges contained in the dipole (imagine the simple dipole composed of \(-Q\) and \(+Q\)) to see that\[

U = - \vec d_e\cdot \vec E = - d_e \vec S_e \cdot \vec E.

\] The electric dipole moment may be defined as "whatever multiplies \(\vec E\) by the inner product" to get an interaction term in the total energy. The expression (including the minus sign) is analogous to the magnetic dipole moment \(\vec m\) that adds \(-\vec m\cdot \vec B\) to the energy.

So far, we were thinking of the world as if it were non-relativistic and classical. If we switch to quantum field theory which is relativistic and quantum mechanical, the expression for the potential energy above is replaced by an interaction term in the Hamiltonian or, in our case, the Lagrangian\[

\LL_{\rm EDM} = -i d_e \cdot \bar\psi_e \sigma^{\mu\nu}\gamma_5 \psi_e \cdot \partial_\mu A_\nu

\] You see that it is similar to the usual interaction term \(\bar\psi\psi\cdot A\) which would have a dimensionless constant \(e\). However, in the dipole case, there is an extra derivative \(\partial_\mu\) in front of the gauge potential which makes the interaction "non-renormalizable" and the coefficient \(d_e\) has the units of length (like the electric dipole: the electric charge is treated as a dimensionless quantity).

If you substitute the non-relativistic (low-speed) form of the spinor \(\psi_e\) and the gauge field and calculate the expectation value of the operator above in a one-electron state of quantum field theory, the Lagrangian reduces to the expression for the potential energy \(U\) above.

Great. So is this electric dipole nonzero? And if it is, how large is it?

The first thing you should notice is that the spin \(\vec S\) is an axial vector while the electric dipole moment is an ordinary, polar vector. So if one is proportional to the other, the theory will fail or refuse (depending on your ethical preferences) to be symmetric under P, the parity. Imagine that the electron is spinning like a wheel of your bike while you are riding; imagine that the electron is the wheel. By the right hand rule, the spin (angular momentum) vector goes to the left side from the wheel's axis. But it's really just a (right hand) convention: Why should the charge of the electron be concentrated on the left side away from the bike? The left side and the right side were equally good to start with. This "unintuitive" asymmetry arises when the parity P is violated.

A bigger problem or audacity is that it violates CP (and therefore the time reversal T) as well (these microscopic violations of T have nothing whatsoever to do with the "cause" of the thermodynamic or logical arrow of time!).

So the underlying theory has to violate P and CP for the coefficient \(d_e\) to be nonzero. In a CP-invariant theory, we would derive \(d_e=0\). Fortunately, the Standard Model is violating CP, a little bit, because of the complex phase in the CKM matrix, the unitary matrix transforming the upper quark mass eigenstates to the upper \(SU(2)\) partners of the lower quark mass eigenstates.

However, this CP-violation only materializes if the quarks of all three generations "show up" in some way. How can it affect the electron? Well, it affects the electron because the quarks of all three generations may emerge as "virtual particles". When you draw the "simplest" Feynman diagram which is not too simple, you will find out that the Standard Model implies that the electron has an electric dipole moment comparable to\[

d_e \approx 10^{-40} e\cdot {\rm m}

\] or slightly smaller. If you divide it by the charge \(e\), you will see that the separation between the electron's "center of mass" and electron's "center of charge" is nonzero but extremely tiny: \(10^{-40}\) meters. That's approximately \(10^{30}\) times shorter than the atomic radius and... \(100,000\) times shorter than the Planck length. (In spite of the misconceptions held by defenders of loop quantum gravity and similar childish "paradigms" about the quantum spacetime constructed out of a Planckian LEGO, there is absolutely nothing wrong if similar quantities with the units of length are shorter than the Planck length. This coefficient is just a universal constant that may have any value and that may manifest itself in experiments with any precision.)

Clearly, you probably can't measure it in your kitchen. Even the world's best experimenters are very far from being able to measure the electric dipole moments that are this tiny.

The new 2013 upper bound on the electric dipole moment assures us that\[

|d_e|\leq 0.87\times 10^{-32}e \cdot {\rm m}.

\] It's a small number but it's \(10^{8}\) i.e. 100 million times greater than the Standard Model value. Once again, the experimenters are telling us that the dipole moment is smaller than 100 million times the Standard Model value. That's not shocking at all for those who believe that the Standard Model is the "whole" story: one is indeed smaller than 100 million so what's the big deal?

There is a lot of room in the middle. The dipole moment may be smaller than 100 million times the Standard Model prediction but it may still be larger than the Standard Model prediction. For example, it may be 10,000 times larger than the Standard Model prediction (due to new physics) which is still 10,000 times smaller than the experimental upper bound (the maximum value allowed by the restrictions-loving experimenters).

Garden variety new physics

However, the experimental bounds are not quite useless because new physics "around the corner" could be able to produce much stronger sources of CP violation that is larger than 100 million times the Standard Model value! How large is the dipole moment according to a "garden variety" mode of new physics? Well, it may be estimated as\[

d_e\approx c\frac{m_e}{16\pi^2 M^2}

\] where the constant \(c\) is comparable to \(1\) if we adopt the type of "true garden variety" popular among many phenomenologists. However, there may be very good reasons why a model implies that \(c\ll 1\).

Why did we include all the factors? The factor \(1/16\pi^2\) (it is \(0.00633\) but many of us would still agree that it is a "number of order one"!) is a "one-loop factor" that always appears in one-loop diagrams and a Feynman diagram contributing to the dipole has to have at least one loop.

The expression is proportional to the electron mass \(m_e\) because almost any leading correction to the dipole moment depends on "both 2-component spinors" that are included in the electron's Dirac field and their leading interaction is proportional to \(m_e\).

Finally, \(1/M^2\) is a power of the "scale where new physics appears" and it must be there for dimensional reasons, to return the units of length (i.e. inverse mass if we use \(c=\hbar=1\) and we do) to the dipole moment. One may justify this \(1/M^2\) in various ways – optimally, from the general arguments of the "Renormalization Group"; or from direct integrals over momentum volumes scaling like powers of \(M\) and propagators going like \(1/M\) or \(1/M^2\) (fermions/bosons) in the loop diagrams, and so on.

At any rate, the estimate is OK for a large class of "garden variety" models of new physics. How large the dipole is? I have already mentioned that \(1/16\pi^2\approx 0.00633\) so including \(c\) slightly smaller than one, we get \(10^{-3}\). The new physics may (but doesn't have to) emerge at \(M\sim 100\GeV\) or \(M\sim 1\TeV\).

For the extreme \(100\GeV\) case – being excluded (or discovered) while you're reading these lines (well, when the LHC starts again) – the ratio \(m_e/M\) is of order \(1/100,000\); recall that the electron mass is half an \(\MeV\). When multiplied by \(10^{-3}\) encountered earlier, we get \(10^{-8}\). And in the units of meters, \(100\GeV\) is inverse to \(10^{-18}\) meters or so; that's the distance scale that the current colliders are already safely probing. So when this distance is multiplied by \(10^{-8}\), we get about \(10^{-26}\) meters.

That's about the maximum value you may get from "maximally CP-violating" physics that is only "starting" to be excluded by the LHC. The ACME upper bound is \(10^{-32}\) meters so it is almost 1 million times stricter and more nontrivial. The new electron electric dipole moment upper bound surely excludes "maximally CP-violating, utterly generic new physics" not only at the scale \(100\GeV\) but even at scales \(10\TeV\) and perhaps a bit higher. If a god told us that the new physics has to be generic and maximally CP-violating (offering no tricks to suppress the CP-violation relatively to the simple estimate above), the ACME result would tell us much more about the non-existence or "huge distance" of new physics than the LHC.



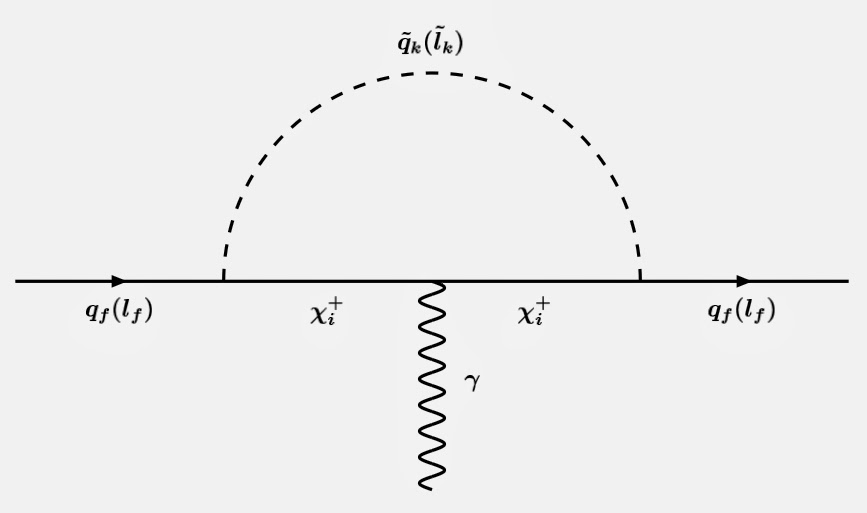
Check the post by Jester who is among those who think that they have already heard this particular god speaking. His blog post ends with an estimate of an "unrefined" garden variety supersymmetric model. The Feynman diagram above which contributes to the electric dipole of a quark (or lepton) and exploits a one-loop process with virtual charginos and a virtual slepton (or squark) is taken from Jester's blog.

Prof Matt Strassler has only written one sentence about the ACME experiment.

SUSY, new physics has no reason to be "garden variety"

Well, I don't really trust this estimate. I don't think that the ACME result really implies that the LHC isn't allowed to discover new physics in the 2015- run (and the chances at the Very Large Hadron Collider would be even higher, of course). The reason is that there may be very natural cancellations that make the constant above \(c\lll 1\). This is also – or particular – true for SUSY.

In fact, the people who have known me for a decade or so know that I have always considered moderately small dimensionless constants of order \(1/1,000\) etc. to be just fine. In fact, I have always believed that we ultimately have lots of experimental evidence for some hierarchies and large or small dimensionless ratios – so their origin has to be "somewhere" (and whether the largeness or smallness is "explained" anthropically doesn't really matter here; what matters is that they exist). A more refined understanding may always render an estimate by dimensional analysis naive.

In fact, I have never considered the "purpose" of SUSY to be to provide us with a "totally generic garden variety model of new physics". SUSY is very constrained. It is actually giving us many cancellations and that's one of the main reasons of its importance. The cancellations don't seem to directly apply to the constant \(c\) above but there are other cancellations and other patterns and mechanisms that, in combination with supersymmetry, may make \(c\) very small, too.

For a (slightly randomly chosen) discussion of the status of naturalness in SUSY and ways by which SUSY models solve the CP-problems like the dangerous overgrown dipole moment as well as flavor problems (transformations of fermions from one generation to another that are also predicted to be much faster by "garden variety new physics" than the experimental bounds allow), I recommend you this 2 months old paper by Arvanitaki et al.

The Last Vestiges of Naturalness

They conclude that even if superpartners are discovered at the LHC in 2015, "naturalness will not emerge triumphant". Well, I think it has been non-triumphant for some years and I have never seen any reasons why it should "triumph". For me, naturalness is just a vague guide, a non-rigorous or Bayesian way to direct us. Due to its probabilistic and ignorance-dependent character, it is not an unbreakable principle of physics. So it's just fine if naturalness fails to emerge triumphant or if it will be shown to be pretty much a loser.

On the other hand, I do care about SUSY, I am sure it's there in Nature, and I find it sufficiently important to know whether or not it's close enough to be discovered by the LHC (or other experiments). The key point is that the positive motivation for SUSY is still with us and some classes of models are naturally compatible with the small CP-violating parameters (like the dipole moment discussed here) and the small flavor-violating parameters as well as with a tolerable degree of residual fine-tuning for the Higgs mass.

Arvanitaki et al. summarize the literature on "viable SUSY models" (in the sense of the previous sentence) as a composite of three classes of models or ideas:

1. split families (unfortunately and confusingly called "natural SUSY" by many physicists)
2. baryonic R-parity violation
3. Dirac gauginos

These scenarios have been discussed on this blog repeatedly, especially the last two and mostly for theoretical reasons, not so much because of the purely phenomenological upper bounds or obsession with naturalness. But again: What do these possibilities mean and why they're viable?

Split families

The split families are often called "natural SUSY". I don't like this phrase because while this scenario is motivated by some general ideas about naturalness (in a modern technical sense), the adjective reveals some hype because the name is meant to make you believe that it's the only way how naturalness may be incorporated (it's not, see e.g. the other two options in the list) and it doesn't really respect the long-term meaning of the word "natural" that keeps on evolving as our relation to Nature's own naturalness is becoming increasingly intimate (we are refining our knowledge of Nature's "discrete rules" and improving our "rough estimates").

At any rate, the split family models were actually introduced long before the LHC began its collisions. They want to make the cancellations of the Higgs mass etc. "natural" and it's good to have light superpartners for that but the proponents of these models noticed that not all superpartners are equally important to achieve this goal. In particular, it's only the third generation and gluinos (and electroweakinos) whose lightness is important for the lightness of the Higgs boson.

The first two generations may be much heavier. Because their interaction with the Higgs boson is much weaker (that's reflected by the much lower mass of the light generations of fermions – after the Higgs takes on a nonzero vev) – they don't influence the Higgs mass (and its lightness and the related Higgs fine-tuning) too much. So the first two generations of leptons and quarks (selectron, smuon, two sneutrinos, sup, sdown, sstrange, and scharm) may be allowed to be heavy; physicists like to say that these two generations "decouple" (they're not "localized" at the same energy scale).

This discriminatory treatment of the first two generations is also good because of the recent LHC constraints. The LHC has shown that too light superpartners don't exist. However, the first two generations are much more constrained than the third generation. It's because it's much easier (or "it would be much easier" if they existed) to produce the first (and, to just slightly lesser extent, second) generation of quarks and leptons (because the protons are composed of the first generation and the conversion to the second generation is relatively easy).

Quantitatively, we know that the first two generations of squarks are heavier than something comparable to several or \(10\TeV\). The third-generation leptons and/or quarks (stop, sbottom, stau, and one sneutrino) may still be lighter than \(1\TeV\) (the bounds on the gluino are something like \(1.2\TeV\) now). This segregated attribution of mass to the quarks and leptons is good because it allows particles "maximum freedom to be heavy" while not spoiling the Higgs' lightness; it is a generic way to agree with the current, "non-uniform" upper bounds; but we get some extra advantages, too.

Because of the gap, the flavor-changing processes are automatically suppressed i.e. the counterpart of the constant \(c\ll 1\). We may imagine that the grouped generations allow us to define a new \(U(1)\) group under which the third generation has a different charge than the first two – this construction may be made literal and visualized as different locations of the generations on different branes in a (stringy) braneworld. So we get some new (approximate) conservation laws, so to say, and the flavor-changing processes are discouraged.

For similar reasons, the split families also reduce all the CP-violating parameters such as \(c,d_e\) relevant for the dipole moment we discuss here. You know from the CKM matrix that the CP-violating phases depend on the mixing of many fields (three generations in the case of quarks) and if two generations are "qualitatively segregated" from the third one (in the case of squarks), the mixing between the first two and the third one is reduced which may also reduce the CP-violating phase.

Baryonic RPV

In most of the model building, it's still being assumed that the R-parity which is equal to\[

P_R = (-1)^{2J+B-L}

\] for the MSSM particles (it's \(+1\) for all the Standard Model particles and \(-1\) for their superpartners: check it, it is easy) is exactly conserved. Such a conservation has a virtue – the lightest \(P_R=-1\) particle, the LSP (lightest superpartner), is exactly stable and may be assumed to be the particle of dark matter.

However, the R-parity may also be violated in which case Nature allows the \(P_R=-1\) particles to decay to \(P_R=+1\) particles only. If that's so, the LSP isn't stable but the gravitino may play the role of the dark matter instead because its decay is very slow, mostly due to the weakness of gravity (which dictates the strength of gravitino's interactions, too).

This improves the naturalness simply because the LHC events with a large "missing energy" (=ultimately LSP) are erased because the LSP decays to well-known particles. Consequently, RPV (R-parity violating) models become compatible with the LHC data even if the superpartners are much lighter than allowed in R-parity-conserving models. See a 2011 text on some RPV models; there have been several others.

Because of the formula for \(P_R\) above and because of the "unbreakable" conservation of the spin (which follows from the rotational symmetry; but the conservation of the spin modulo one, i.e. the conservation of the statistics, is an even more unbreakable law), the R-parity violation requires to violate either the conservation of the baryon number \(B\) or the lepton number \(L\) or both, too. If both are violated, we're in trouble because it becomes easy for the proton to decay to a positron and some neutral junk. We know from the "futile" searches for decaying protons that this decay is either non-existent or (more likely) so slow that the relevant term in the Lagrangian is so tiny that it can't matter for the LHC physics.

So in viable models, the R-parity violation may occur through lepton-number-violating terms only; or through baryon-number-violating terms only. The experimental tests seem to be much more tolerant to baryon-number-violating, R-parity-violating terms like the superpotential\[

{\mathcal W}_{bRPV} = \frac{\lambda''_{ijk}}{2} U^c_i D^c_j D^c_k.

\] Such an operator may destroy up, down, down (s)quarks in some combination. In some sense, it's able to destroy a "sneutron" and convert it to pure energy. The electric charge and overall color (none) is conserved but the baryon number jumps by \(\pm 1\). There are some other reasons why the baryon RPV (bRPV) models seem more attractive than lepton-number-violating RPV models and why they became popular in the very fresh literature.

At any rate, they allow the superpartners to be much lighter – these lighters superpartners become largely invisible at the LHC because they don't produce missing energy (stable LSP) in the decays. This improves the situation of the Higgs lightness fine-tuning. The CP (e.g. electron electric dipole moment) and flavor problems aren't solved too well, as far as I know, and the baryon violation may also cripple baryogenesis. This puts a pressure on the gravitino mass from both sides (a few \(\GeV\) is marginally OK) and none of the values seems really great, despite some improvements that hidden sectors may bring.

But when one focuses on the degree of "unexplained fine-tuning" needed to avoid a contradiction with the empirical bounds (if it can be avoided at all), this class of models seems less contrived than garden-variety models of new physics, too.

Dirac gauginos

I have discussed Dirac gauginos in many articles. If the gauginos (superpartners of the gauge bosons) are Dirac fermions, they contain not just one two-component Majorana (or Weyl) spinor but two. Because of the \(\NNN=1\) SUSY, the second one must be paired with a boson and it can't be a \(j=1\) vector boson anymore because a gauge group may only support one vector field; instead, it must be a \(j=0\) scalar.

Consequently, such gauginos belong to a pair of multiplets (chiral supermultiplet and vector supermultiplet) which may be combined into the \(\NNN=2\) vector multiplet. That sounds great because the gauge fields and their pals could actually show us more supersymmetry than the minimal amount, some extended supersymmetry. I have argued that such extended supersymmetry (eight conserved supercharges) could follow from a braneworld description of gauge fields in string theory. Extended supersymmetry is surely cool and stringy; after all, it's the (even more extended) \(\NNN=4\) supersymmetry that the Yang-Mills fields are given if people study the most popular example of the AdS/CFT (even if they use it as a model for QCD).

The Dirac gluinos also improve the situation in many purely phenomenological questions. They may be much heavier than the usual Majorana gluinos – and still allow the Higgs lightness to be pretty natural. Flavor-changing dangerous processes are slowed down because they depend on the Majorana mass and this parameter may be made much smaller (basically zero) now. The gluino exchange in the \(t\)-channel decreases more quickly at higher energies so that the production of squarks is predicted to be less frequent. This reduces the potential contradictions with the LHC constraints, too. I don't know what new sources of CP-violation are doing; I don't really expect them to be too suppressed because we're switching to more "complex/Weyl" fields and those like to produce CP-violating phases.

To summarize this section, there are several proposed "pretty structures" on top of supersymmetry that may make many if not all of the potential "problems of garden-variety new physics" or at least "problems of general SUSY models" go away. These extra ideas are not as profound as the idea of supersymmetry itself but they're still pretty cute and they could finally turn out to be the right explanations why some naive estimates of new effects by dimensional analysis are (very) inaccurate.

New physics may be relatively close and it may be far. We don't really know. We may exclude some particular models of "nearby new physics" while others remain viable. There are vague arguments that may support each possible answer. Because the option "no new physics almost anywhere" is pretty much understood (it's been studied as "the Standard Model" for 40 years), it's logical that both experimenters and (pheno-oriented) theorists focus on the other option that assumes some new physics. The ACME experiment is telling us something – under some assumptions, it is telling us "more" about new physics than the whole LHC; with some other assumptions, it's telling us about some "qualitative properties" of the new physics that aren't so terribly new or surprising.

Many of the contemporary theoretical arguments, ideas, and mechanisms are neat and clever and Nature may very well be exploiting one of them or several of them – or some other insights that may be found by the theorists in the near or far future. Some of these "extra structures" have the potential to tell us about the way by which string theory is realized in the Universe, e.g. about the shape and our (and different particles') location within the extra dimensions.

Stay tuned.